
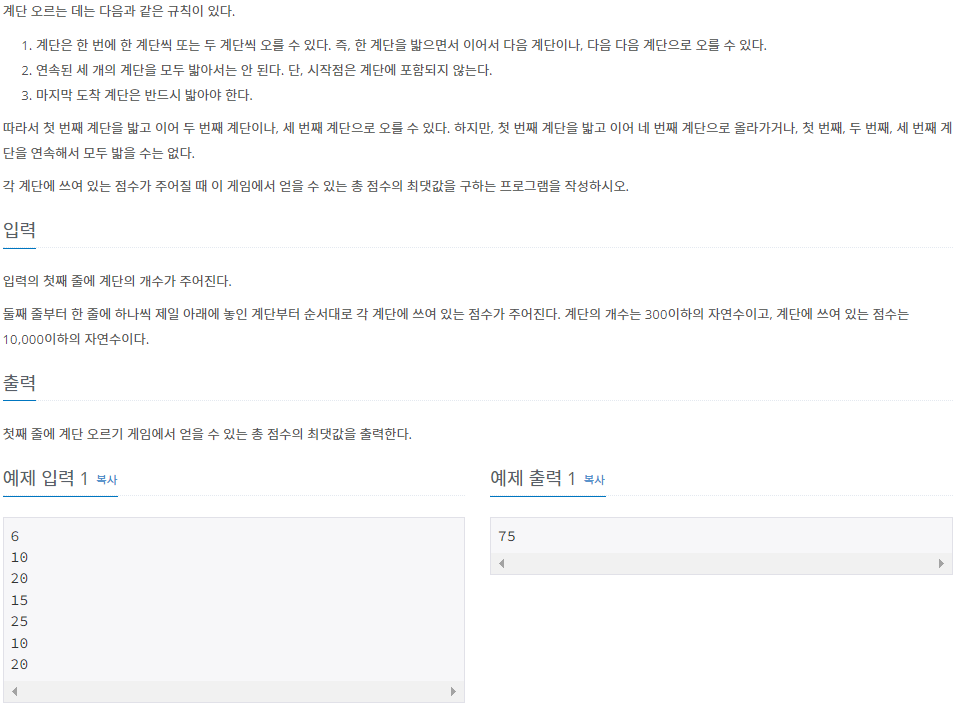
각각 점수가 부여된 계단을 규칙에 따라 올랐을 때 얻을 수 있는 총 점수의 최댓값을 구하는 문제다.
규칙은 다음과 같다.
- 계단은 한 번에 한 계단 또는 두 계단 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다.
- 마지막 계단은 반드시 밟아야 한다.
규칙 3을 기준으로 나머지 규칙을 적용하면 가능한 몇가지의 경우의 수를 얻을 수 있다.
n-5 | n-4 | n-3 | n-2 | n-1 | n
^ - 마지막 계단을 반드시 밟아야 한다.
^ ^ ^ - 경우의 수 1. (n-3)계단과 (n-1)계단을 밟고 온다.
^ ^ - 경우의 수 2. (n-2)계단을 밟고 온다.
- 경우의 수 1에 대해 N 번째 계단에서 얻을 수 있는 최대 점수(dp[N]) 는 N번째 계단의 점수와 직전 계단의 점수, 및 N-3 번째 계단까지 올라오는데 얻을 수 있는 최대점수(dp[N-3])의 합이다.
최대점수[N] = 계단점수[N] + 계단점수[N-1] + 최대점수[N-3]
- 경우의 수 2에 대해 N번째 계단에서 얻을 수 있는 최대 점수는 N번째 계단의 점수와 N-2번째 계단까지 올라오는데 얻을 수 있는 최대 점수(dp[N-3])의 합으로 나타낼 수 있을 것이다.
최대점수[N] = 계단점수[N] + 최대점수[N-2]
이 두 경우의 수 중, 우리는 최대값을 얻어야 하므로 다음과 같이 나타낼 수 있다.
dp[N] = Math.max(경우의 수 1, 경우의 수 2)
import java.util.Scanner;
public class Main {
static int[] steps;
static int[] dp;
public static void main (String[] args){
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
steps = new int[t+1]; // 계단
dp = new int[t+1]; // 최대점수
for(int i = 1; i<=t; i++){
steps[i] = sc.nextInt();
}
dp[0] = 0; // 0번째 계단에서 얻을 수 있는 최대 점수
dp[1] = steps[1];
if (t >= 2) {
dp[2] = steps[1] + steps[2];
}
for (int i =3; i<=t; i++){
dp[i] = Math.max(steps[i-1] + dp[i-3], dp[i-2]) + steps[i];
}
System.out.println(dp[t]);
}
}'Algorithm' 카테고리의 다른 글
| 백준 9184번 신나는 함수 실행 (0) | 2023.03.15 |
|---|---|
| 백준 11053번 가장 긴 증가하는 부분 수열 (0) | 2023.03.15 |
| 백준 1003번 피보나치 함수 (1) | 2023.03.14 |
| 백준 1010번 다리 놓기 (0) | 2023.03.14 |
| 백준 2231번 분해합 (0) | 2023.03.13 |




댓글